When differences in significance aren’t significant differences

“We compared treatments A and B with a placebo. Treatment A showed a significant benefit over placebo, while treatment B had no statistically significant benefit. Therefore, treatment A is better than treatment B.”

We hear this all the time. It’s an easy way of comparing medications, surgical interventions, therapies, and experimental results. It’s straightforward. It seems to make sense.

However, a difference in significance does not always make a significant difference.²²

One reason is the arbitrary nature of the \(p < 0.05\) cutoff. We could get two very similar results, with \(p = 0.04\) and \(p = 0.06\), and mistakenly say they’re clearly different from each other simply because they fall on opposite sides of the cutoff. The second reason is that p values are not measures of effect size, so similar p values do not always mean similar effects. Two results with identical statistical significance can nonetheless contradict each other.

Instead, think about statistical power. If we compare our new experimental drugs Fixitol and Solvix to a placebo but we don’t have enough test subjects to give us good statistical power, then we may fail to notice their benefits. If they have identical effects but we have only 50% power, then there’s a good chance we’ll say Fixitol has significant benefits and Solvix does not. Run the trial again, and it’s just as likely that Solvix will appear beneficial and Fixitol will not.

Instead of independently comparing each drug to the placebo, we should compare them against each other. We can test the hypothesis that they are equally effective, or we can construct a confidence interval for the extra benefit of Fixitol over Solvix. If the interval includes zero, then they could be equally effective; if it doesn’t, then one medication is a clear winner. This doesn’t improve our statistical power, but it does prevent the false conclusion that the drugs are different. Our tendency to look for a difference in significance should be replaced by a check for the significance of the difference.

Examples of this error in common literature and news stories abound. A huge proportion of papers in neuroscience, for instance, commit the error.⁴⁴ You might also remember a study a few years ago suggesting that men with more biological older brothers are more likely to be homosexual.⁹ How did they reach this conclusion? And why older brothers and not older sisters?

The authors explain their conclusion by noting that they ran an analysis of various factors and their effect on homosexuality. Only the number of older brothers had a statistically significant effect; number of older sisters, or number of nonbiological older brothers, had no statistically significant effect.

But as we’ve seen, that doesn’t guarantee that there’s a significant difference between the effects of older brothers and older sisters. In fact, taking a closer look at the data, it appears there’s no statistically significant difference between the effect of older brothers and older sisters. Unfortunately, not enough data was published in the paper to allow a direct calculation.²²

When significant differences are missed

The problem can run the other way. Scientists routinely judge whether a significant difference exists simply by eye, making use of plots like this one:

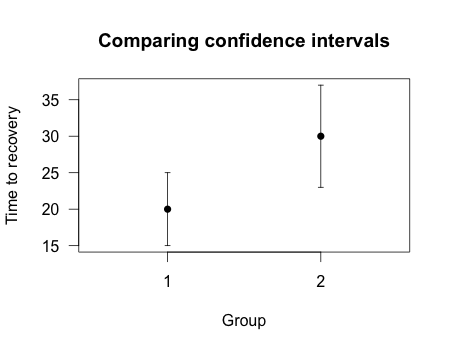
Imagine the two plotted points indicate the estimated time until recovery from some disease in two different groups of patients, each containing ten patients. There are three different things those error bars could represent:

1. The standard deviation of the measurements. Calculate how far each observation is from the average, square each difference, and then average the results and take the square root. This is the standard deviation, and it measures how spread out the measurements are from their mean.
2. The standard error of some estimator. For example, perhaps the error bars are the standard error of the mean. If I were to measure many different samples of patients, each containing exactly n subjects, I can estimate that 68% of the mean times to recover I measure will be within one standard error of “real” average time to recover. (In the case of estimating means, the standard error is the standard deviation of the measurements divided by the square root of the number of measurements, so the estimate gets better as you get more data – but not too fast.) Many statistical techniques, like least-squares regression, provide standard error estimates for their results.
3. The confidence interval of some estimator. A 95% confidence interval is mathematically constructed to include the true value for 95 random samples out of 100, so it spans roughly two standard errors in each direction. (In more complicated statistical models this may not be exactly true.)

These three options are all different. The standard deviation is a simple measurement of my data. The standard error tells me how a statistic, like a mean or the slope of a best-fit line, would likely vary if I take many samples of patients. A confidence interval is similar, with an additional guarantee that 95% of 95% confidence intervals should include the “true” value.

In the example plot, we have two 95% confidence intervals which overlap. Many scientists would view this and conclude there is no statistically significant difference between the groups. After all, groups 1 and 2 might not be different – the average time to recover could be 25 in both groups, for example, and the differences only appeared because group 1 was lucky this time. But does this mean the difference is not statistically significant? What would the p value be?

In this case, \(p< 0.05\). There is a statistically significant difference between the groups, even though the confidence intervals overlap.[1]

Unfortunately, many scientists skip hypothesis tests and simply glance at plots to see if confidence intervals overlap. This is actually a much more conservative test – requiring confidence intervals to not overlap is akin to requiring \(p < 0.01\) in some cases.⁵⁰ It is easy to claim two measurements are not significantly different even when they are.

Conversely, comparing measurements with standard errors or standard deviations will also be misleading, as standard error bars are shorter than confidence interval bars. Two observations might have standard errors which do not overlap, and yet the difference between the two is not statistically significant.

A survey of psychologists, neuroscientists and medical researchers found that the majority made this simple error, with many scientists confusing standard errors, standard deviations, and confidence intervals.⁶ Another survey of climate science papers found that a majority of papers which compared two groups with error bars made the error.³⁷ Even introductory textbooks for experimental scientists, such as An Introduction to Error Analysis, teach students to judge by eye, hardly mentioning formal hypothesis tests at all.

There are, of course, formal statistical procedures which generate confidence intervals which can be compared by eye, and even correct for multiple comparisons automatically. For example, Gabriel comparison intervals are easily interpreted by eye.¹⁹

Overlapping confidence intervals do not mean two values are not significantly different. Similarly, separated standard error bars do not mean two values are significantly different. It’s always best to use the appropriate hypothesis test instead. Your eyeball is not a well-defined statistical procedure.

[1]	This was calculated with an unpaired t test, based on a standard error of 2.5 in group 1 and 3.5 in group 2.