Stopping rules and regression to the mean

Medical trials are expensive. Supplying dozens of patients with experimental medications and tracking their symptoms over the course of months takes significant resources, and so many pharmaceutical companies develop “stopping rules,” which allow investigators to end a study early if it’s clear the experimental drug has a substantial effect. For example, if the trial is only half complete but there’s already a statistically significant difference in symptoms with the new medication, the researchers may terminate the study, rather than gathering more data to reinforce the conclusion.

When poorly done, however, this can lead to numerous false positives.

For example, suppose we’re comparing two groups of patients, one with a medication and one with a placebo. We measure the level of some protein in their bloodstreams as a way of seeing if the medication is working. In this case, though, the medication causes no difference whatsoever: patients in both groups have the same average protein levels, although of course individuals have levels which vary slightly.

We start with ten patients in each group, and gradually collect more data from more patients. As we go along, we do a t test to compare the two groups and see if there is a statistically significant difference between average protein levels. We might see a result like this simulation:

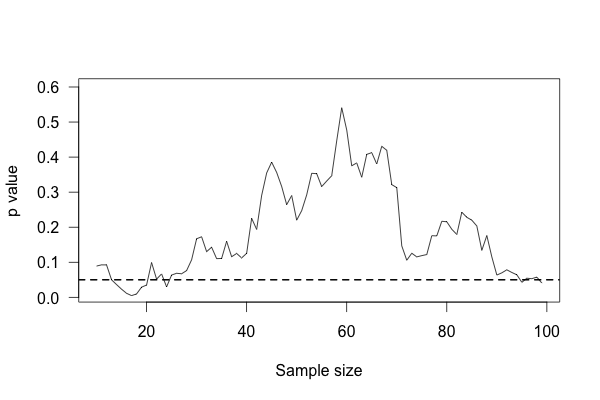
This plot shows the p value of the difference between groups as we collect more data, with the horizontal line indicating the \(p = 0.05\) level of significance. At first, there appears to be no significant difference. Then we collect more data and conclude there is. If we were to stop, we’d be misled: we’d believe there is a significant difference between groups when there is none. As we collect yet more data, we realize we were mistaken – but then a bit of luck leads us back to a false positive.

You’d expect that the p value dip shouldn’t happen, since there’s no real difference between groups. After all, taking more data shouldn’t make our conclusions worse, right? And it’s true that if we run the trial again we might find that the groups start out with no significant difference and stay that way as we collect more data, or start with a huge difference and quickly regress to having none. But if we wait long enough and test after every data point, we will eventually cross any arbitrary line of statistical significance, even if there’s no real difference at all. We can’t usually collect infinite samples, so in practice this doesn’t always happen, but poorly implemented stopping rules still increase false positive rates significantly.⁵³

Modern clinical trials are often required to register their statistical protocols in advance, and generally pre-select only a few evaluation points at which they test their evidence, rather than testing after every observation. This causes only a small increase in the false positive rate, which can be adjusted for by carefully choosing the required significance levels and using more advanced statistical techniques.⁵⁶ But in fields where protocols are not registered and researchers have the freedom to use whatever methods they feel appropriate, there may be false positive demons lurking.

Truth inflation

Medical trials also tend to have inadequate statistical power to detect moderate differences between medications. So they want to stop as soon as they detect an effect, but they don’t have the power to detect effects.

Suppose a medication reduces symptoms by 20% over a placebo, but the trial you’re using to test it does not have adequate statistical power to detect this difference. We know that small trials tend to have varying results: it’s easy to get ten lucky patients who have shorter colds than usual, but much harder to get ten thousand who all do.

Now imagine running many copies of this trial. Sometimes you get unlucky patients, and so you don’t notice any statistically significant improvement from your drug. Sometimes your patients are exactly average, and the treatment group has their symptoms reduced by 20% – but you don’t have enough data to call this a statistically significant increase, so you ignore it. Sometimes the patients are lucky and have their symptoms reduced by much more than 20%, and so you stop the trial and say “Look! It works!”

You’ve correctly concluded that your medication is effective, but you’ve inflated the size of its effect. You falsely believe it is much more effective than it really is.

This effect occurs in pharmacological trials, epidemiological studies, gene association studies (“gene A causes condition B”), psychological studies, and in some of the most-cited papers in the medical literature.^{30, 32} In fields where trials can be conducted quickly by many independent researchers (such as gene association studies), the earliest published results are often wildly contradictory, because small trials and a demand for statistical significance cause only the most extreme results to be published.³³

As a bonus, truth inflation can combine forces with early stopping rules. If most drugs in clinical trials are not quite so effective to warrant stopping the trial early, then many trials stopped early will be the result of lucky patients, not brilliant drugs – and by stopping the trial we have deprived ourselves of the extra data needed to tell the difference. Reviews have compared trials stopped early with other studies addressing the same question which did not stop early; in most cases, the trials stopped early exaggerated the effects of their tested treatments by an average of 29%.³

Of course, we do not know The Truth about any drug being studied, so we cannot tell if a particular study stopped early due to luck or a particularly good drug. Many studies do not even publish the original intended sample size or the stopping rule which was used to justify terminating the study.⁴³ A trial’s early stoppage is not automatic evidence that its results are biased, but it is a suggestive detail.

Little extremes

Suppose you’re in charge of public school reform. As part of your research into the best teaching methods, you look at the effect of school size on standardized test scores. Do smaller schools perform better than larger schools? Should you try to build many small schools or a few large schools?

To answer this question, you compile a list of the highest-performing schools you have. The average school has about 1,000 students, but the top-scoring five or ten schools are almost all smaller than that. It seems that small schools do the best, perhaps because of their personal atmosphere where teachers can get to know students and help them individually.

Then you take a look at the worst-performing schools, expecting them to be large urban schools with thousands of students and overworked teachers. Surprise! They’re all small schools too.

What’s going on? Well, take a look at a plot of test scores vs. school size:

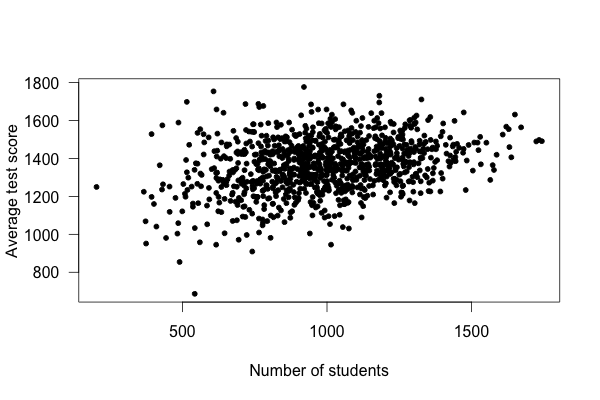
Smaller schools have more widely varying average test scores, entirely because they have fewer students. With fewer students, there are fewer data points to establish the “true” performance of the teachers, and so the average scores vary widely. As schools get larger, test scores vary less, and in fact increase on average.

This example used simulated data, but it’s based on real (and surprising) observations of Pennsylvania public schools.⁵⁹

Another example: In the United States, counties with the lowest rates of kidney cancer tend to be Midwestern, Southern and Western rural counties. How could this be? You can think of many explanations: rural people get more exercise, inhale less polluted air, and perhaps lead less stressful lives. Perhaps these factors lower their cancer rates.

On the other hand, counties with the highest rates of kidney cancer tend to be Midwestern, Southern and Western rural counties.

The problem, of course, is that rural counties have the smallest populations. A single kidney cancer patient in a county with ten residents gives that county the highest kidney cancer rate in the nation. Small counties hence have vastly more variable kidney cancer rates, simply because they have so few residents.²¹